10109. Tree Минимальная глубина

Дано бинарное дерево. Найдите его минимальную глубину. Минимальной глубиной называется количество вершин в кратчайшем пути от корня до ближайшего листа.

Определение дерева:

//Java

class TreeNode {

int val;

TreeNode left;

TreeNode right;

TreeNode(int x) {

val = x;

left = null;

right = null;

}

}

// C++

class TreeNode

{

public:

int val;

TreeNode *left;

TreeNode *right;

TreeNode(int x) : val(x), left(NULL), right(NULL) {}

};

Реализуйте функцию minDepth которая возвращает минимальную глубину дерева.

// Java

int minDepth (TreeNode tree)

// C++

int minDepth(TreeNode *tree)

Пример

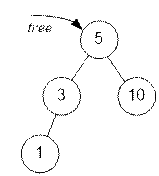
Функция minDepth возвращает 2, так как кратчайший путь от корня 5 до ближайшего листа 10 содержит 2 вершины.

РЕШЕНИЕ

дерево

Анализ алгоритма

Если tree = NULL, то минимальная глубина дерева равна 0.

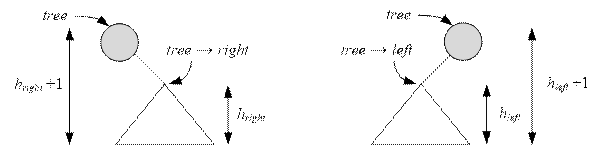
Если у дерева нет левого сына, то минимальная глубина дерева равна минимальной глубине правого поддерева плюс 1.

Если у дерева нет правого сына, то минимальная глубина дерева равна минимальной глубине левого поддерева плюс 1.

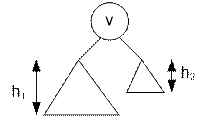
Иначе вычисляем минимальную глубину левого h₁ и правого h₂ поддерева и возвращаем значение min(h₁, h₂) + 1.

Реализация алгоритма

int minDepth(TreeNode* tree)

{

Если tree = NULL, то минимальная глубина дерева равна 0.

if (tree == NULL) return 0;

Если у дерева нет левого сына, то минимальная глубина дерева равна минимальной глубине правого поддерева плюс 1.

if (tree->left == NULL)

return minDepth(tree->right) + 1;

Если у дерева нет правого сына, то минимальная глубина дерева равна минимальной глубине левого поддерева плюс 1.

if (tree->right == NULL)

return minDepth(tree->left) + 1;

Вычисляем минимальную глубину левого Left и правого Right поддерева. Возвращаем значение min(Left, Right) + 1.

int Left = minDepth(tree->left);

int Right = minDepth(tree->right);

return min(Left, Right) + 1;

}

Java реализация

int minDepth(TreeNode tree)

{

if (tree == null) return 0;

if (tree.left == null)

return minDepth(tree.right) + 1;

if (tree.right == null)

return minDepth(tree.left) + 1;

int Left = minDepth(tree.left);

int Right = minDepth(tree.right);

return Math.min(Left, Right) + 1;

}